Transformer Blog
- self-attention method
- multi-head attention
- transformer structure
- position embedding
- position encoding
- Transformer structure
- mask
reference links which helps a lot:
import numpy as np
import matplotlib.pyplot as plt
import torch
from torch import nn
import torch.nn.functional as F

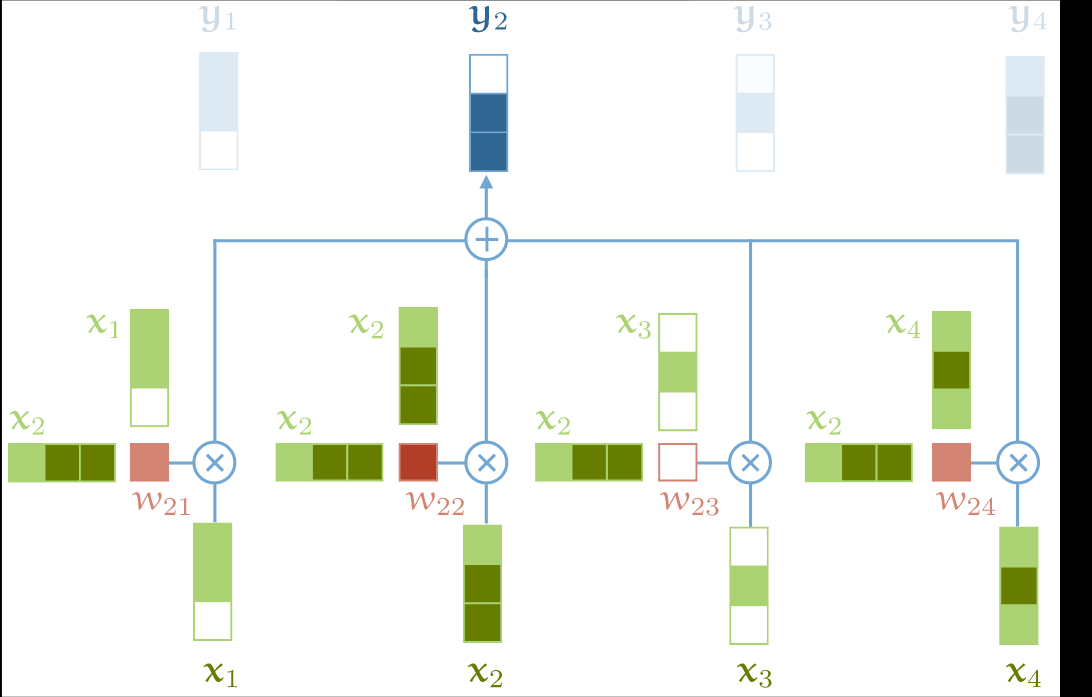
x = torch.randn(2,3,4)
raw_weights = torch.bmm(x,x.transpose(1,2))
weights = F.softmax(raw_weights,dim=2)
weights
y = torch.bmm(weights,x)
y
torch.random.seed()
temp = torch.randint(0,2,(2,2))
temp
yy = F.softmax(temp.float(),dim=0)
yy
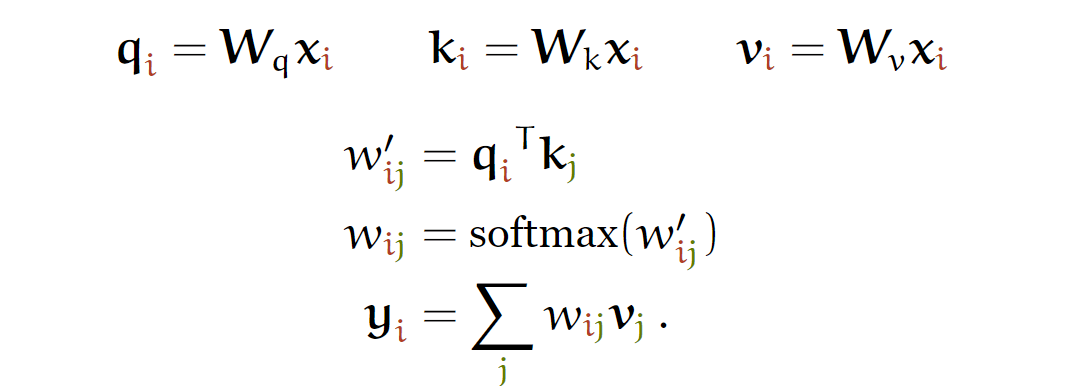
aa = np.random.randint(1,10,(3,4))
aa
aa[:,0::2]
class SelfAttentionWide(nn.Module):
def __init__(self, emb, heads=8, mask=False):
"""
:param emb:
:param heads:
:param mask:
"""
super().__init__()
self.emb = emb
self.heads = heads
self.mask = mask
self.tokeys = nn.Linear(emb, emb * heads, bias=False)
self.toqueries = nn.Linear(emb, emb * heads, bias=False)
self.tovalues = nn.Linear(emb, emb * heads, bias=False)
self.unifyheads = nn.Linear(heads * emb, emb)
def forward(self, x):
b, t, e = x.size()
h = self.heads
assert e == self.emb, f'Input embedding dim ({e}) should match layer embedding dim ({self.emb})'
keys = self.tokeys(x) .view(b, t, h, e)
queries = self.toqueries(x).view(b, t, h, e)
values = self.tovalues(x) .view(b, t, h, e)
# compute scaled dot-product self-attention
# - fold heads into the batch dimension
keys = keys.transpose(1, 2).contiguous().view(b * h, t, e)
queries = queries.transpose(1, 2).contiguous().view(b * h, t, e)
values = values.transpose(1, 2).contiguous().view(b * h, t, e)
queries = queries / (e ** (1/4))
keys = keys / (e ** (1/4))
# - Instead of dividing the dot products by sqrt(e), we scale the keys and values.
# This should be more memory efficient
# - get dot product of queries and keys, and scale
dot = torch.bmm(queries, keys.transpose(1, 2))
assert dot.size() == (b*h, t, t)
if self.mask: # mask out the upper half of the dot matrix, excluding the diagonal
mask_(dot, maskval=float('-inf'), mask_diagonal=False)
dot = F.softmax(dot, dim=2)
# - dot now has row-wise self-attention probabilities
# apply the self attention to the values
out = torch.bmm(dot, values).view(b, h, t, e)
# swap h, t back, unify heads
out = out.transpose(1, 2).contiguous().view(b, t, h * e)
return self.unifyheads(out)
class SelfAttentionNarrow(nn.Module):
def __init__(self, emb, heads=8, mask=False):
"""
:param emb:
:param heads:
:param mask:
"""
super().__init__()
assert emb % heads == 0, f'Embedding dimension ({emb}) should be divisible by nr. of heads ({heads})'
self.emb = emb
self.heads = heads
self.mask = mask
s = emb // heads
# - We will break the embedding into `heads` chunks and feed each to a different attention head
self.tokeys = nn.Linear(s, s, bias=False)
self.toqueries = nn.Linear(s, s, bias=False)
self.tovalues = nn.Linear(s, s, bias=False)
self.unifyheads = nn.Linear(heads * s, emb)
def forward(self, x):
b, t, e = x.size()
h = self.heads
assert e == self.emb, f'Input embedding dim ({e}) should match layer embedding dim ({self.emb})'
s = e // h
x = x.view(b, t, h, s)
keys = self.tokeys(x)
queries = self.toqueries(x)
values = self.tovalues(x)
assert keys.size() == (b, t, h, s)
assert queries.size() == (b, t, h, s)
assert values.size() == (b, t, h, s)
# Compute scaled dot-product self-attention
# - fold heads into the batch dimension
keys = keys.transpose(1, 2).contiguous().view(b * h, t, s)
queries = queries.transpose(1, 2).contiguous().view(b * h, t, s)
values = values.transpose(1, 2).contiguous().view(b * h, t, s)
queries = queries / (e ** (1/4))
keys = keys / (e ** (1/4))
# - Instead of dividing the dot products by sqrt(e), we scale the keys and values.
# This should be more memory efficient
# - get dot product of queries and keys, and scale
dot = torch.bmm(queries, keys.transpose(1, 2))
assert dot.size() == (b*h, t, t)
if self.mask: # mask out the upper half of the dot matrix, excluding the diagonal
mask_(dot, maskval=float('-inf'), mask_diagonal=False)
dot = F.softmax(dot, dim=2)
# - dot now has row-wise self-attention probabilities
# apply the self attention to the values
out = torch.bmm(dot, values).view(b, h, t, s)
# swap h, t back, unify heads
out = out.transpose(1, 2).contiguous().view(b, t, s * h)
return self.unifyheads(out)
we can also change the code using einsum which help to short the code part and have a nice execution time https://rockt.github.io/2018/04/30/einsum
class SelfAttentionWideEinsum(nn.Module):
def __init__(self, emb, heads=8, mask=False):
"""
:param emb:
:param heads:
:param mask:
"""
super().__init__()
self.emb = emb
self.heads = heads
self.mask = mask
self.tokeys = nn.Linear(emb, emb * heads, bias=False)
self.toqueries = nn.Linear(emb, emb * heads, bias=False)
self.tovalues = nn.Linear(emb, emb * heads, bias=False)
self.unifyheads = nn.Linear(heads * emb, emb)
def forward_einsum(self, x):
b, t, e = x.size()
h = self.heads
keys = self.tokeys(x).view(b, t, h, e)
queries = self.toqueries(x).view(b, t, h, e)
values = self.tovalues(x).view(b, t, h, e)
dot = torch.einsum('bthe,bihe->bhti', queries, keys) / math.sqrt(e)
dot = F.softmax(dot, dim=-1)
out = torch.einsum('bhtd,bdhe->bthe', dot, values)
# we can move reshape of weights to init; I left it here just to compare with the original implementation
out = torch.einsum('bthe,khe->btk', out, self.unifyheads.weight.view(e,h,e))
return out + self.unifyheads.bias
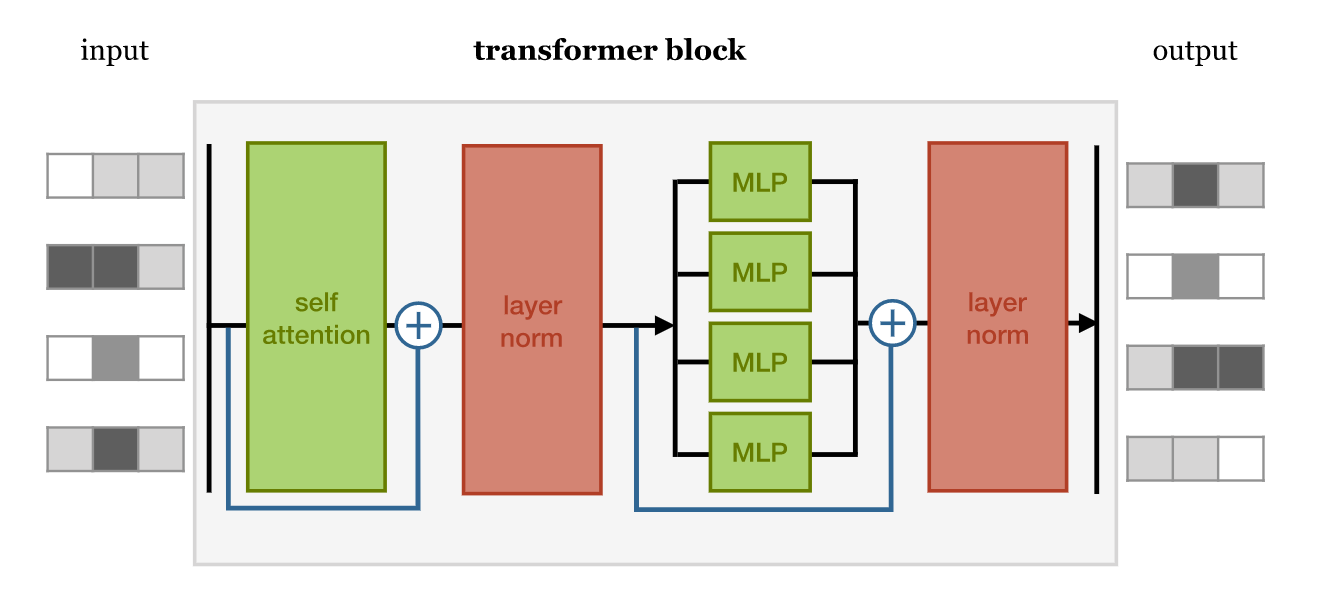
class TransformerBlock(nn.Module):
def __init__(self, emb, heads, mask, seq_length, ff_hidden_mult=4, dropout=0.0, wide=True):
super().__init__()
self.attention = SelfAttentionWide(emb, heads=heads, mask=mask) if wide \
else SelfAttentionNarrow(emb, heads=heads, mask=mask)
self.mask = mask
self.norm1 = nn.LayerNorm(emb)
self.norm2 = nn.LayerNorm(emb)
'''
We’ve made the relatively arbitrary choice of making the hidden layer
of the feedforward 4 times as big as the input and output. Smaller values may work as well,
and save memory, but it should be bigger than the input/output layers.
'''
self.ff = nn.Sequential(
nn.Linear(emb, ff_hidden_mult * emb),
nn.ReLU(),
nn.Linear(ff_hidden_mult * emb, emb)
)
self.do = nn.Dropout(dropout)
def forward(self, x):
attended = self.attention(x)
x = self.norm1(attended + x)
x = self.do(x)
fedforward = self.ff(x)
x = self.norm2(fedforward + x)
x = self.do(x)
return x
def d(tensor=None):
"""
Returns a device string either for the best available device,
or for the device corresponding to the argument
:param tensor:
:return:
"""
if tensor is None:
return 'cuda' if torch.cuda.is_available() else 'cpu'
return 'cuda' if tensor.is_cuda else 'cpu'
temp = torch.randn(2,3,4)
temp
>>> # an Embedding module containing 10 tensors of size 6
>>> embedding = nn.Embedding(10, 6)
>>> # a batch of 2 samples of 4 indices each
>>> input = torch.LongTensor([[1,2,3]])
>>> embedding(input)
temp[None,:,:].shape
b,t,e = 3,5,6
position = nn.Embedding(10,6)(torch.arange(t))[None, :, :].expand(b, t, e)
position
# Code from https://www.tensorflow.org/tutorials/text/transformer
def get_angles(pos, i, d_model):
angle_rates = 1 / np.power(10000, (2 * (i//2)) / np.float32(d_model))
return pos * angle_rates
def positional_encoding(position, d_model):
angle_rads = get_angles(np.arange(position)[:, np.newaxis],
np.arange(d_model)[np.newaxis, :],
d_model)
# apply sin to even indices in the array; 2i
angle_rads[:, 0::2] = np.sin(angle_rads[:, 0::2])
# apply cos to odd indices in the array; 2i+1
angle_rads[:, 1::2] = np.cos(angle_rads[:, 1::2])
pos_encoding = angle_rads[np.newaxis, ...]
return pos_encoding
tokens = 10
dimensions = 64
pos_encoding = positional_encoding(tokens, dimensions)
print (pos_encoding.shape)
plt.figure(figsize=(12,8))
plt.pcolormesh(pos_encoding[0], cmap='viridis')
plt.xlabel('Embedding Dimensions')
plt.xlim((0, dimensions))
plt.ylim((tokens,0))
plt.ylabel('Token Position')
plt.colorbar()
plt.show()
class Transformer(nn.Module):
def __init__(self, k, heads, depth, seq_length, num_tokens, num_classes):
super().__init__()
self.num_tokens = num_tokens
self.token_emb = nn.Embedding(num_tokens, k)
self.pos_emb = nn.Embedding(seq_length, k)
# The sequence of transformer blocks that does all the
# heavy lifting
tblocks = []
for i in range(depth):
tblocks.append(TransformerBlock(k=k, heads=heads))
self.tblocks = nn.Sequential(*tblocks)
# Maps the final output sequence to class logits
self.toprobs = nn.Linear(k, num_classes)
def forward(self, x):
"""
:param x: A (b, t) tensor of integer values representing
words (in some predetermined vocabulary).
:return: A (b, c) tensor of log-probabilities over the
classes (where c is the nr. of classes).
"""
# generate token embeddings
tokens = self.token_emb(x)
b, t, k = tokens.size()
# generate position embeddings
positions = torch.arange(t)
positions = self.pos_emb(positions)[None, :, :].expand(b, t, k)
x = tokens + positions
x = self.tblocks(x)
# Average-pool over the t dimension and project to class
# probabilities
x = self.toprobs(x.mean(dim=1))
return F.log_softmax(x, dim=1)
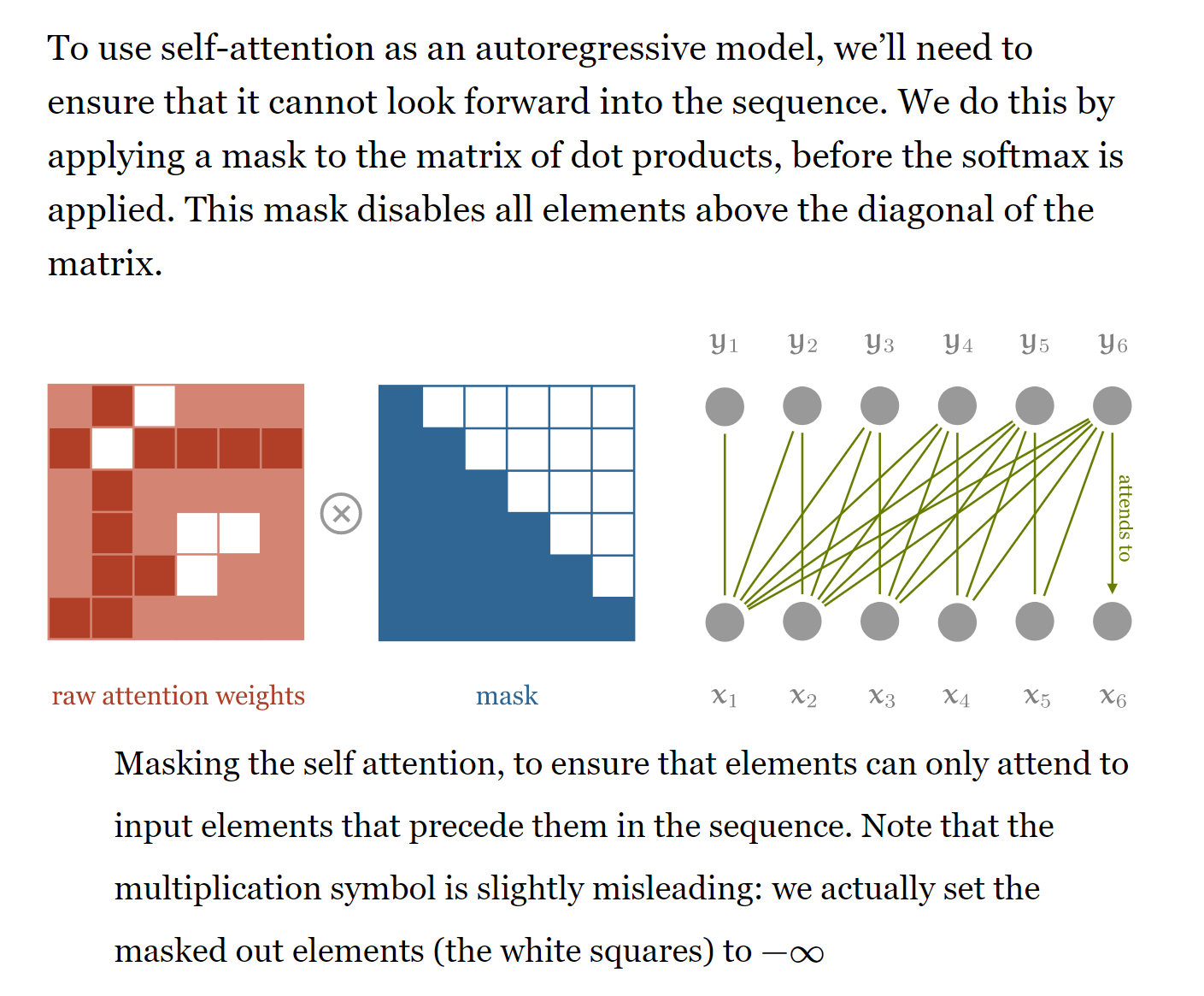
iu1 = np.triu_indices(4)
iu2 = np.triu_indices(4,2)
iu1
# iu2
a = np.arange(16).reshape(4,4)
a[iu1]
a
a[iu2]
iu1 = torch.triu_indices(4,4)
a = torch.arange(16).view(4,4)
a
iu1
a[iu1[0],iu1[1]]
# mask function
def mask_(matrices, maskval=0.0, mask_diagonal=True):
"""
Masks out all values in the given batch of matrices where i <= j holds,
i < j if mask_diagonal is false
In place operation
:param tns:
:return:
"""
b, h, w = matrices.size()
indices = torch.triu_indices(h, w, offset=0 if mask_diagonal else 1)
matrices[:, indices[0], indices[1]] = maskval
queries = torch.randn(1,3,3)
keys = torch.randn(1,3,3)
t = 3
dot = torch.bmm(queries, keys.transpose(1, 2))
indices = torch.triu_indices(t, t, offset=1)
dot[:, indices[0], indices[1]] = float('-inf')
dot = F.softmax(dot, dim=2)
indices
dot
dot[:, indices[0], indices[1]]